|
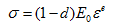
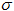 为应力, 为应力, 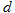 为损伤变量, 为损伤变量, 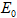 为初始弹性模量, 为初始弹性模量, 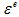 为弹性应变。 为弹性应变。
-
损伤理论采用“刚度折减”的方式,通过引入刚度折减系数,反映(混凝土)材料在外力作用下开裂等引起的软化和弱化特性。
-
采用损伤变量d表示材料损伤、破坏的程度,1-d则为刚度折减系数。
-
损伤变量随着材料受力和变形的变化而改变,其演化和变化的规律由损伤理论经过实验数据拟合确定。
-
不同损伤理论中的损伤变量的具体含义可能不完全相同,计算过程中需要适当换算。
-
损伤可以自然地与构件和结构的整体完整性评估联系起来。
-
李杰教授学术梯队专注混凝土损伤理论的研究已经有十余年的时间,现行规范中的混凝土损伤理论即为李杰教授研究梯队的研究成果。
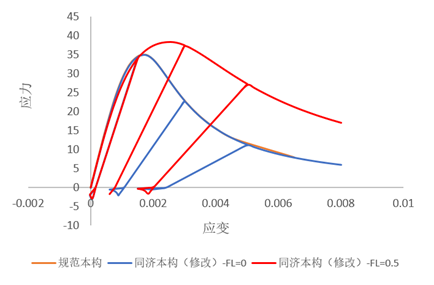
拉压反复作用下单轴应力应变关系曲线
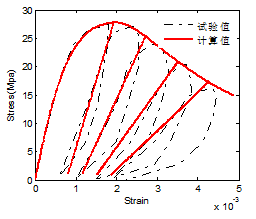 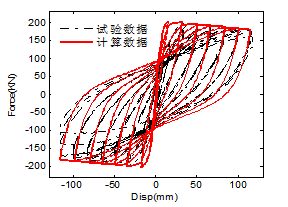
应力-应变曲线力-位移曲线
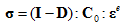
 为应力张量, 为应力张量, 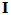 为四阶单位张量, 为四阶单位张量, 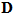 为四阶损伤张量, 为四阶损伤张量, 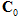 为初始刚度张量, 为初始刚度张量, 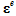 为弹性应变张量。 为弹性应变张量。
-
通过引入张量表达,多轴损伤本构关系和单轴损伤本构关系的表达形式具有一致性,各项的含义也是一致的。
-
多维损伤D是一个四阶张量,其在外部作用下的演化过程较为复杂,需要建立张量方程对其进行表述。
-
多轴本构关系的数值求解较为复杂,需要引入特别的数值分析技术和复杂的算法,一般设计单位很难自行完成这类开发和编程工作。
-
为了表征混凝土在拉、压作用下的迥异特性,引入损伤张量的分解,采用两个损伤标量及其对应的投影张量表征损伤张量,这类模型得到了学术界和工程界的广泛认同,在混凝土多轴受力分析中应用最广。
对于初始损伤相同的两种受力状态,若损伤能释放率相同,则相应的损伤相等。基于这一原理,可以引入能量等效应变,将一维损伤演化规律应用到多维受力状态。
从一维损伤演化到多维损伤演化(能量等效应变)
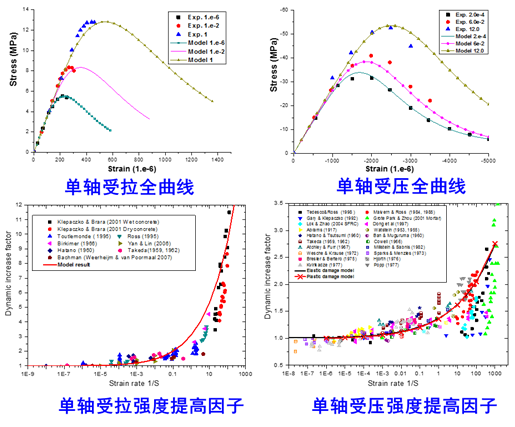
与试验结果对比:
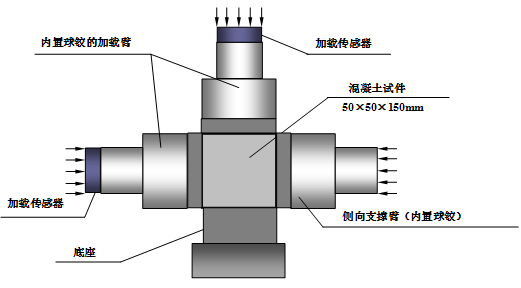
双轴加载试验
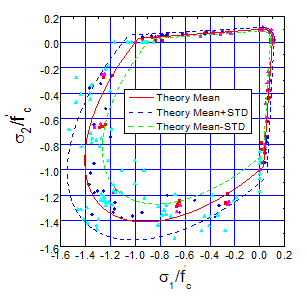
双轴强度包络图
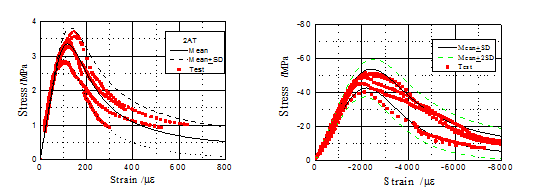
单轴受拉全曲线单轴受压全曲线
分别在损伤子空间和塑性子空间中考虑材料的应变率效应。
损伤子空间理论
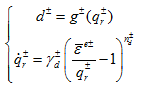
塑性子空间理论
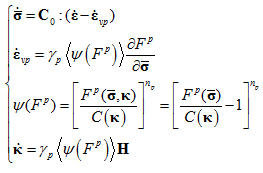
-
新版《混凝土结构设计规范》(GB50010-2010)对本构关系的修订
基于上述研究成果(包括李杰、吴建营、杨卫忠和任晓丹的奠基性工作),对于二维受力状态,关于应力主轴可建立如下弹塑性损伤本构关系的矩阵表达式:
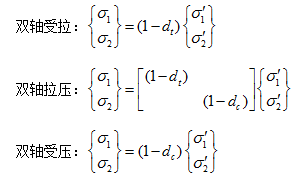
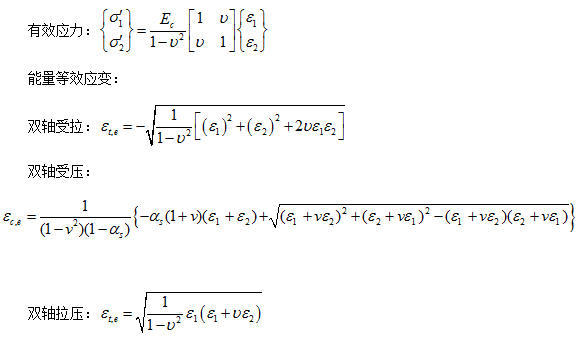
-
多尺度损伤理论(Micro-cracks informed damage model)
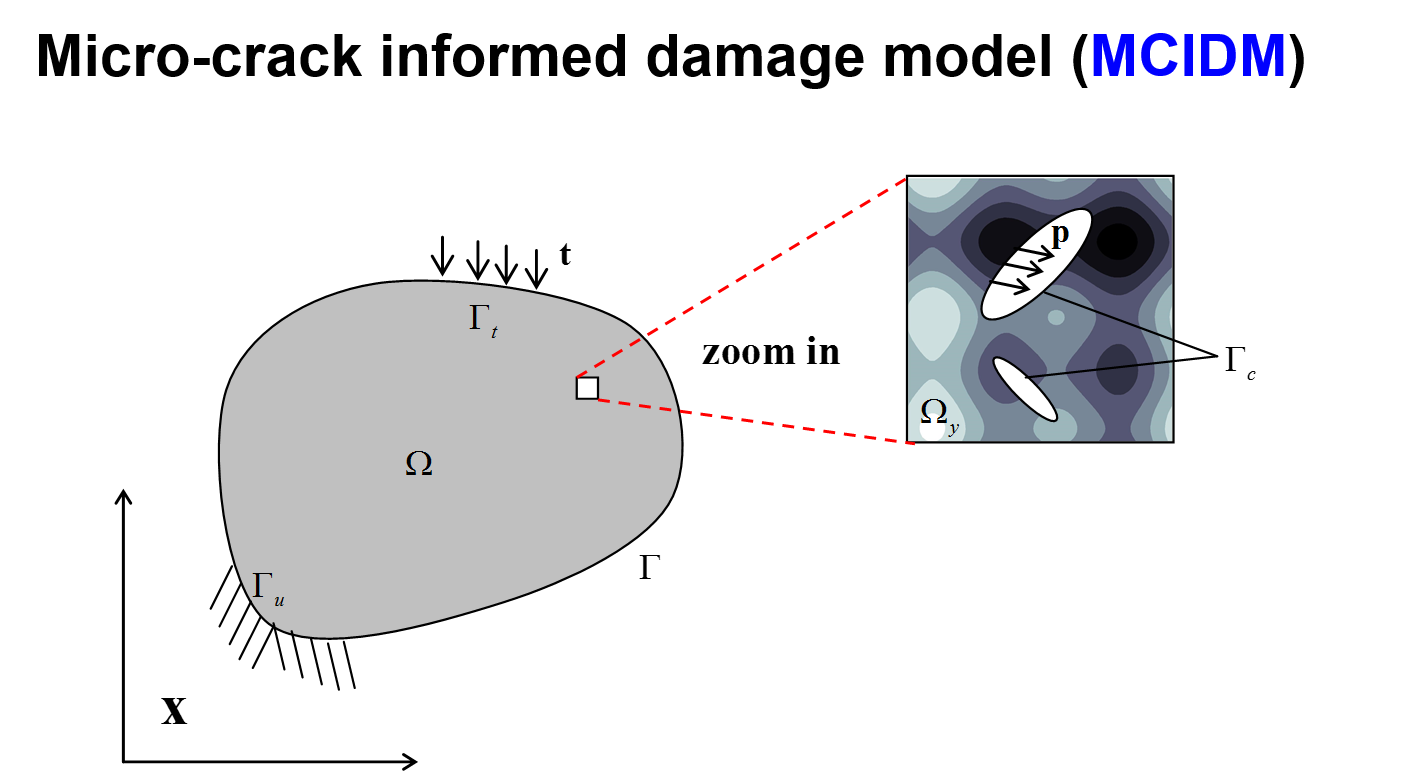
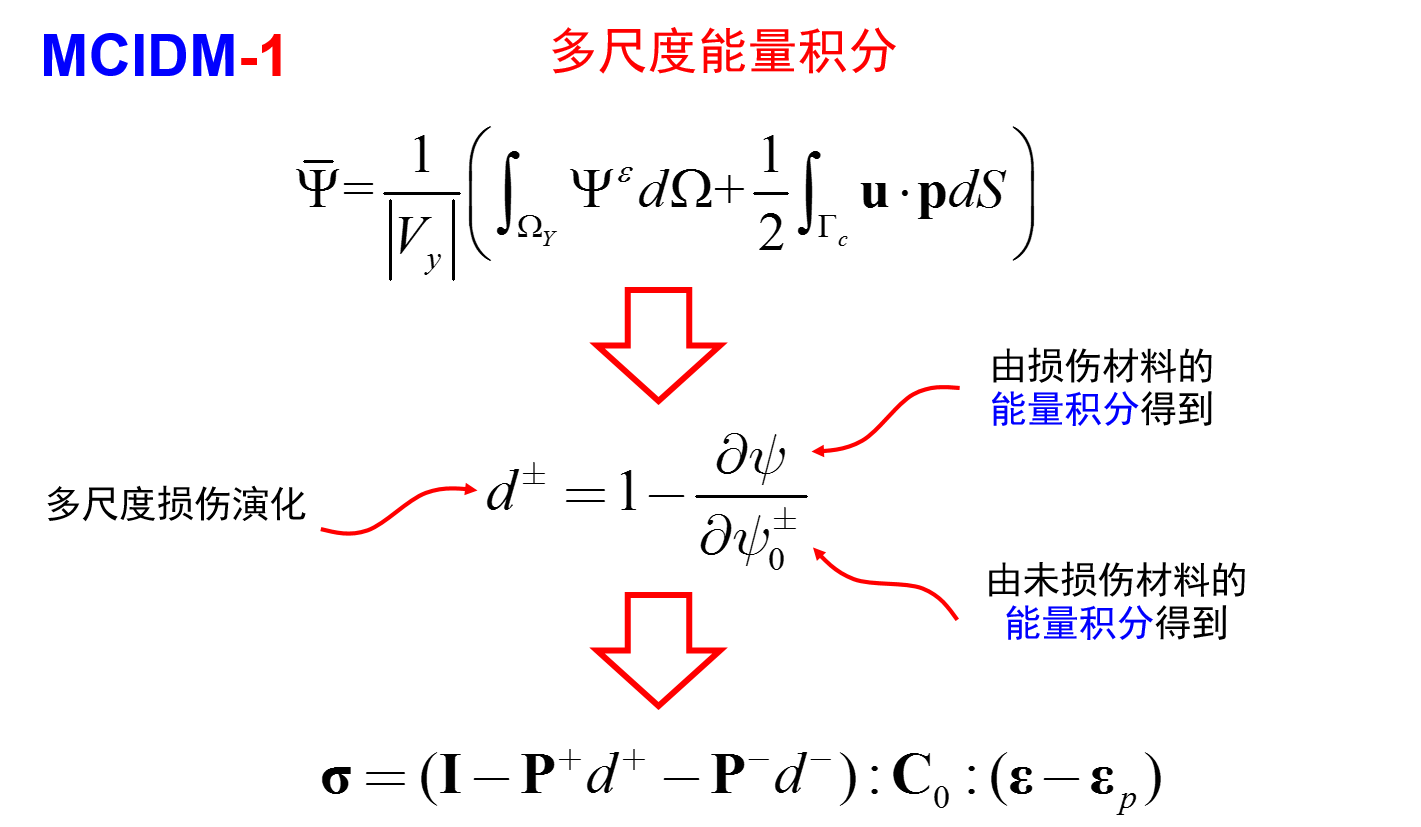
请参已发表的阅相关论文。
|